| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- riot api dart
- leetcode dart
- dart new 키워드
- 발로란트 api dart
- 파이썬 부동소수점
- 파이썬
- swift concurrency
- dart
- swift 동시성
- tft api dart
- flutter
- 롤 api dart
- 롤토체스 api dart
- com.google.GIDSignIn
- flutter widget
- docker overview
- flutter statefulwidget
- PlatformException(sign_in_failed
- AnimationController
- Architectural overview
- flutter ios 폴더
- valorant api dart
- dart new
- lol api dart
- dart.dev
- keychain error
- widget
- flutter bloc
- flutter android 폴더
- generate parentheses dart
- Today
- Total
aspe
ML - Clustering 본문
Clustering
Determining similarity according to a predetermined measure and grouping data with similarity above a threshold.
Prerequisite for Clustering
Proximity measure
Simliarity or Distance.

Criterion function for evalution
A measure of distinguishing between good clustering results and poor results.

Clustering algorithm
Algorithm to optimize the evaluation Criterion function.
Partitional clustering
- K-Means, K-SOM, DBSAN
Hierarchical clustering
- Disivie(top-down), Agglomerative(bottom-up)

K-Means Clustering

Convergence criteria
When there are no more data points to change cluster to another cluster.
When the center of each cluster is no longer changed.
When SSE decreases below a certain standard.
Pros
Simple and easy to implement
Efficient time complexity (o(tkn)) (t : iteration, k : num of clusters, n : num of datas)
Cons
Predetermined k that means number of clusters
Greatly influenced by the initial value.
Vulnerable to outliers. -> Remove outliers or Random sampling
DBSCAN
Algorithm to find any type of cluster by expanding the cluster in consideration of regional density.
It overcame the disadvantages of K-Means, which only allows Hyper-elipsoid-type clusters.

DBSCAN Terms
Eps(epllise)
The radius of the space (circle) to measure the density (user designated)
Density
The number of data points in the Eps space.
Core point
The data points that have larger density then MinPts(minimum density)
Border point
A data point with a density less than MinPts, although it is a neighbor of the core point (which exists in the same Eps space with the core point).
Nosie point
Not core point and border point, but data point.


K-SOM(Kohonen Self Organization Maps)
An artificial neural network that performs clustering by updating weights through competitive learning of the output layer. Learn in a way that can explain input data well.
Competitive step
Select a node that has the largest value (Winner-Takes-All)
Cooperation and adaptation step
Update the weights of neighboring nodes of the winner node.
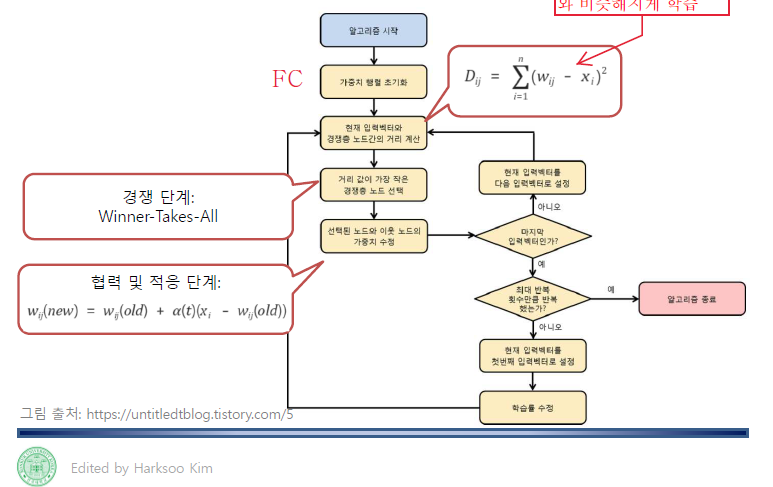
Example

Hierarchical Clustering
It is sometimes ideal in many cases to tie in layers based on density.

Agglomerative Hierarchical Clustering
Initialie with each example in singleton cluster while there is more than 1 cluseter.
1. Find 2 nearest clusters
2. Merge them
Four common ways to measure cluster distance
1. minimum distance

Find minimum distance between clusters.
2. Maximum distance
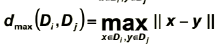
Find maximum distance between clusters.
3. Average distance
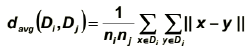
Use average distance of nodes in clusters.
4. Mean distance

This involves finding the mean vector location for each of the clusters and taking the distance between the two centroids.
Single Linkage of Nearest Neightbor

Complete Linkage or Farthest Neighbor

Divisive vs Agglomerative
Divisive Algorithm(top - down)
Since clustering can be performed in consideration of the overall data distribution, optimal space division is possible.
Slow speed
Agglomerative Algorithm(bottom-up)
Fast speed
There is a possibility of performing a local optima due to the failure to consider the overall data distribution.
